Bitruncation

In geometry, a bitruncation is an operation on regular polytopes. It represents a truncation beyond rectification.^{[citation needed]} The original edges are lost completely and the original faces remain as smaller copies of themselves.

Bitruncated regular polytopes can be represented by an extended Schläfli symbol notation t_1,2{p,q,...} or 2t{p,q,...}.

In regular polyhedra and tilings

For regular polyhedra (i.e. regular 3-polytopes), a bitruncated form is the truncated dual. For example, a bitruncated cube is a truncated octahedron.

In regular 4-polytopes and honeycombs

For a regular 4-polytope, a bitruncated form is a dual-symmetric operator. A bitruncated 4-polytope is the same as the bitruncated dual, and will have double the symmetry if the original 4-polytope is self-dual.

A regular polytope (or honeycomb) {p, q, r} will have its {p, q} cells bitruncated into truncated {q, p} cells, and the vertices are replaced by truncated {q, r} cells.

Self-dual {p,q,p} 4-polytope/honeycombs

An interesting result of this operation is that self-dual 4-polytope {p,q,p} (and honeycombs) remain cell-transitive after bitruncation. There are 5 such forms corresponding to the five truncated regular polyhedra: t{q,p}. Two are honeycombs on the 3-sphere, one a honeycomb in Euclidean 3-space, and two are honeycombs in hyperbolic 3-space.

Space	4-polytope or honeycomb	Schläfli symbol Coxeter-Dynkin diagram	Cell type	Cell image	Vertex figure
${\displaystyle \mathbb {S} ^{3}}$	Bitruncated 5-cell (10-cell) (Uniform 4-polytope)	t1,2{3,3,3}	truncated tetrahedron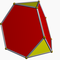
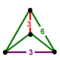
	Bitruncated 24-cell (48-cell) (Uniform 4-polytope)	t1,2{3,4,3}	truncated cube
${\displaystyle \mathbb {E} ^{3}}$	Bitruncated cubic honeycomb (Uniform Euclidean convex honeycomb)	t1,2{4,3,4}	truncated octahedron
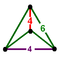
${\displaystyle \mathbb {H} ^{3}}$	Bitruncated icosahedral honeycomb (Uniform hyperbolic convex honeycomb)	t1,2{3,5,3}	truncated dodecahedron
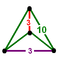
	Bitruncated order-5 dodecahedral honeycomb (Uniform hyperbolic convex honeycomb)	t1,2{5,3,5}	truncated icosahedron

See also

• uniform polyhedron
• uniform 4-polytope
• Rectification (geometry)
• Truncation (geometry)

References

• Coxeter, H.S.M. Regular Polytopes, (3rd edition, 1973), Dover edition, ISBN 0-486-61480-8 (pp. 145–154 Chapter 8: Truncation)
• Norman Johnson Uniform Polytopes, Manuscript (1991)
  • N.W. Johnson: The Theory of Uniform Polytopes and Honeycombs, Ph.D. Dissertation, University of Toronto, 1966
• John H. Conway, Heidi Burgiel, Chaim Goodman-Strauss, The Symmetries of Things 2008, ISBN 978-1-56881-220-5 (Chapter 26)

External links

• Weisstein, Eric W. "Truncation". MathWorld.

Polyhedron operators

• v
• t
• e

Seed	Truncation	Rectification	Bitruncation	Dual	Expansion	Omnitruncation	Alternations
t0{p,q} {p,q}	t01{p,q} t{p,q}	t1{p,q} r{p,q}	t12{p,q} 2t{p,q}	t2{p,q} 2r{p,q}	t02{p,q} rr{p,q}	t012{p,q} tr{p,q}	ht0{p,q} h{q,p}	ht12{p,q} s{q,p}	ht012{p,q} sr{p,q}

This page was last edited on 24 September 2023, at 05:14