Small complex icosidodecahedron

Small complex icosidodecahedron
Type	Uniform star polyhedron
Elements	F = 32, E = 60 (30x2) V = 12 (χ = −16)
Faces by sides	20{3}+12{5}
Coxeter diagram
Wythoff symbol	5 | 3/2 5
Symmetry group	Ih, [5,3], *532
Index references	U-, C-, W-
Dual polyhedron	Small complex icosidodecacron
Vertex figure	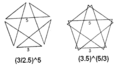(3/2.5)5 (3.5)5/3
Bowers acronym	Cid

In geometry, the small complex icosidodecahedron is a degenerate uniform star polyhedron. Its edges are doubled, making it degenerate. The star has 32 faces (20 triangles and 12 pentagons), 60 (doubled) edges and 12 vertices and 4 sharing faces. The faces in it are considered as two overlapping edges as topological polyhedron.

A small complex icosidodecahedron can be constructed from a number of different vertex figures.

A very similar figure emerges as a geometrical truncation of the great stellated dodecahedron, where the pentagram faces become doubly-wound pentagons ({5/2} --> {10/2}), making the internal pentagonal planes, and the three meeting at each vertex become triangles, making the external triangular planes.

As a compound

The small complex icosidodecahedron can be seen as a compound of the icosahedron {3,5} and the great dodecahedron {5,5/2} where all vertices are precise and edges coincide. The small complex icosidodecahedron resembles an icosahedron, because the great dodecahedron is completely contained inside the icosahedron.

Compound polyhedron

Icosahedron	Great dodecahedron	Compound

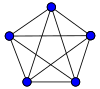
Its two-dimensional analogue would be the compound of a regular pentagon, {5}, representing the icosahedron as the n-dimensional pentagonal polytope, and regular pentagram, {5/2}, as the n-dimensional star. These shapes would share vertices, similarly to how its 3D equivalent shares edges.

Compound polygon

Pentagon	Pentagram	Compound

See also

• Great complex icosidodecahedron
• Small complex rhombicosidodecahedron
• Complex rhombidodecadodecahedron
• Great complex rhombicosidodecahedron

References

• Coxeter, Harold Scott MacDonald; Longuet-Higgins, M. S.; Miller, J. C. P. (1954), "Uniform polyhedra", Philosophical Transactions of the Royal Society of London. Series A. Mathematical and Physical Sciences, 246 (916): 401–450, Bibcode:1954RSPTA.246..401C, doi:10.1098/rsta.1954.0003, ISSN 0080-4614, JSTOR 91532, MR 0062446, S2CID 202575183 (Table 6, degenerate cases)
• Weisstein, Eric W. "Small complex icosidodecahedron". MathWorld.
• Klitzing, Richard. "3D uniform polyhedra x3/2o5o5*a - cid".

This page was last edited on 23 January 2023, at 02:24